What is a Unit Circle?
Astronomy before the telescope
One of the easiest ways to simplify calculations when you don’t have computers or calculators at your fingertips, only tables, with sine and cosine for every .5 degrees, is to reduce it all down to the smallest unit that you will be utilizing.
Since we are talking astronomy, this means that the observations that you make will be taken from a place on the Earth. You must be able to diagram what you have observed in order to perform the trigonometry necessary to calculate distances, etc.
The ONLY method available to perform this task is to make observations and determine the angles to celestial bodies relative to one another. Then you draw a diagram so that you can use trigonometry to find other angles and distances.
The most efficient way to use angular measurements in tandem with the sphere you are standing on, is to use the Earth’s radius as a “unit circle”.
Meaning you simply set the Earth’s radius to 1. So instead of the radius being 860 German miles or 6371 kilometers, it is simply 1.
This is still in use today with the Astronomical Unit. Instead of ~150Mkm, they use 1AU. It is simply a scaling factor that simplifies the math.
Distance to the Moon
The distance to the Moon is not disputed in any model you look at. So if the Moon’s apogee (furthest distance) is 405,500km then using Earth’s radius as a ‘unit’ we simply divide 405,500/6371:
Now the Renaissance astronomers could more easily perform their calculation using these ‘unit’ values to simplify the math.
This is a valuable method for us today, even if we are using CAD. A drawing is much less unwieldy when you don’t have hundreds of millions of kilometer to contend with. It also makes recreating and checking old diagrams much easier when using the same units, while staying at the proper scale.
The Historical Astronomical Unit
Up until the 18th century the distance between the Earth and the Sun did not vary by very much. Longomontanus’ value was 1288 Earth semi-diameters for the mean distance, the AU. (Tycho’s was slightly less than that)
Comparing Models
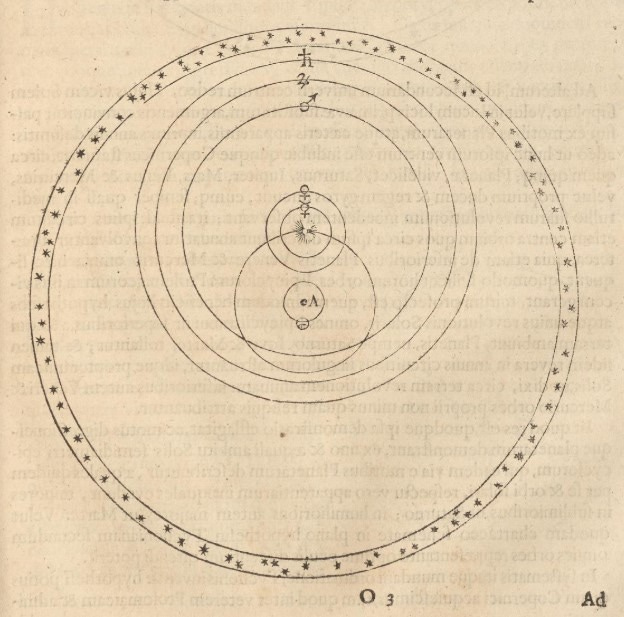
The image below is the representation of Tycho Brahe’s model. The circles representing the orbits of the planets, Sun and Moon (actually the Moon’s orbit is exaggerated in this diagram, for clarity I imagine) are shown in their proper proportionality.
Now remember, there is no debate about the size and distance of/to the Moon. So the orbit that you see here encompassing Earth at letter A is proportional, in Tycho’s/Longomontanus’ model, to the size of the Sun’s orbit, Mercury’s, Venus, etc.
Recall, there are 1288 Earth semi-diameters (radii), making up an AU, in other words the radius of the Sun’s orbit. About 8.24Mkm in Longomontanus’ case.
Now what happens when we apply the Standard Model’s “unit” value to this same diagram.
First we take the modern value of the AU ~150Mkm and we divide that by the radius of the Earth.
Let’s call that a ‘unit’ of 1:23,500.
Remember, Longomontanus had a ‘unit’ ratio of 1:1288 for the Sun’s orbital radius.
So in this case we have to account for the 1288 ‘units’ so we divide 23500 by 1288.
Since I am using AutoCAD, I won’t scale everything up, I have to keep the Earth and Moon’s sizes the same. I will scale everything else though, using Earth’s center as the scaling point.
Now what happens when we scale up the the AU? The Earth and the Moon’s orbit disappear!
At this scale, compared to the AU the orbit of the Moon is barely visible! In fact, the standard model has the size of the Sun at nearly twice the diameter of the Moon’s entire orbit! It’s like the statue of David with the head the size of a pea!
It goes against common sense and is simply a scheme devised by the Royal Society to fool you into believing you are no more than an insignificant ape on a mediocre rock in a ho-hum solar system in the middle of nowhere probably about to collide with a comet that will wipe us out just like the dinosaurs!
That’s a load of baloney so don’t believe it! You are in your rightful place on Earth, the center of the of World and you are special.


Hey, great read as always, it’s truly amazing how such a simple abstraction like the unit circle fundamentally simplifys complex real-world calculatiions, making big problems tractable.